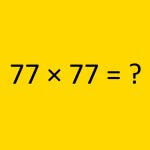小学生でも「18×17」が暗算できる「おみやげ算」のヒミツとは?中3数学の「展開公式」を使って解説(2023.4.18 All About)
という記事を読んだ。
「18 × 17 = ?」のような2桁どうしの掛け算がかんたん計算できる。
「18 × 17」をふつうに暗算で計算するのは難しいが、上記記事で紹介されている「おみやげ算」を使えば正確に暗算できる。
「おみやげ算」の方法
「18 × 17」を「おみやげ算」で解いてみる。
17の一の位の「7」をおみやげとして18に渡す。
おみやげをもらった18は7を加えて25となり、おみやげをわたした17は10となる。
おみやげの授受後の数字(25と10)を掛けて、最後に1の位どうしを掛けたものをたす。
つまり、
25 × 10 + 8 × 7 = 250 + 56 = 306
と、かんたんに暗算できる。
計算が簡単になる理由は、おみやげの受け渡しによって「25 × 10」や「8 × 7」のように「簡単な計算」に変換できるからだ。
おみやげ算のカラクリ
十の位が1どうしの掛け算を考える。
一の位をa, bとすると、
(10 + a)(10 + b)
を計算することになる。
展開すると、
(10 + a)(10 + b) = 100 + 10a + 10b + ab
(10 + b)からbをおみやげとして(10 + a)に渡したものを計算すると、
(10 + a + b)(10 + b – b)
= (10 + a + b) × 10
= 100 + 10a + 10b
この計算結果に一の位どうしの掛け算「ab」をたすと、
100 + 10a + 10b + ab
となり、(10 + a)(10 + b)の答えとなる。
※おみやげ算は「19 × 19」までの掛け算に使える。